三平方の定理とは？基本を押さえよう

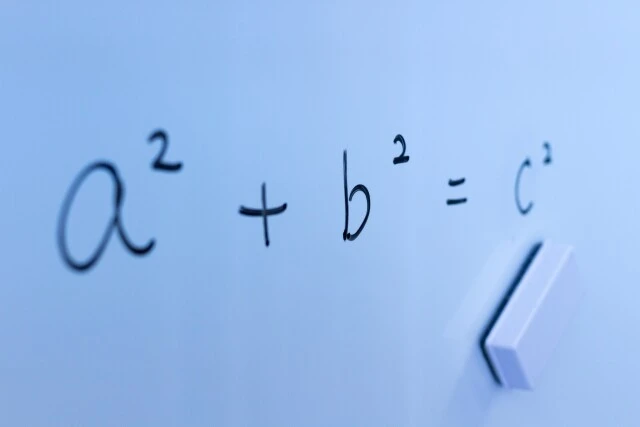
平方の定理は、直角三角形の2辺と斜辺の関係を示す重要な定理であり「ピタゴラスの定理」とも呼ばれます。

三平方の定理の公式は「a²＋b²＝c²」で、2辺の長さがわかれば残りの1辺を簡単に計算できます。定理に直角三角形の3辺を当てはめる場合は、一番長い斜辺をcとするのがポイントです。

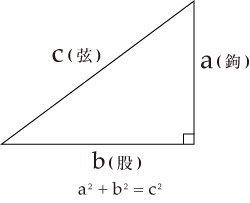
画像引用：国立図書館「コラム ピタゴラスの定理｜江戸の数学」

三平方の定理は、直角三角形の基本的な性質をあらわしており、数学において多くの問題に応用できます。

また、定理は逆にも適用できるため、三角形の3辺がa²＋b²＝c²である場合、三角形が直角三角形であると示すことが可能です。

たとえば、a = 3、 b = 4の直角三角形の場合、斜辺の長さは次のように求められます。

c²＝3²＋4²

c²= 9+16

c²= 25

c =√25

c = 5

このように、斜辺の長さが簡単に求められます。

また、xy平面上の2点間の距離を求める際にも、三平方の定理は便利です。今後もさまざまな問題に活用するため、しっかりと公式を覚えましょう。

三平方の定理の証明方法

三平方の定理には、100以上の証明方法があるとされていますが、

なかでも代表的でわかりやすいのが「正方形を用いた証明」です。

正方形を用いた証明では、図形の面積を使って三平方の定理の公式を導き出します。
 

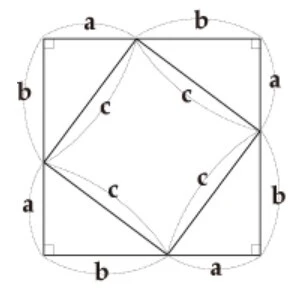
画像引用：国立図書館「コラム ピタゴラスの定理｜江戸の数学」

1辺の長さがa+bの大きな正方形を考え、その中に1辺がcの小さな正方形を配置します。ここで、外側と内側の正方形の面積を求めてみましょう。

大きな正方形の面積は(a+b)²、小さな正方形の面積はc²です。また、4つの直角三角形の面積はそれぞれ1/2abなので、1/2ab×4で合計は2abになります。

上記で求めた値を「外側の正方形の面積-4つの直角三角形の合計面積 = 内側の正方形の面積」の式に当てはめると、以下のようになります。

(a+b)²－2ab＝c²
a²＋2ab＋b²－2ab＝c²
a²＋b²＝c²

a²＋b²＝c²となり、三平方の定理の証明ができました。

図形の面積を使って三平方の定理を視覚的に理解する方法は、数学のほかの分野の問題を解く際にも役立ちます。複雑な問題にも応用できるので、ぜひ三平方の定理の証明方法を理解しておきましょう。

三平方の定理で覚えておきたい重要ポイント4つを紹介

三平方の定理で覚えておきたい重要ポイントは、以下の4つです。

1. 特別な直角三角形を覚える
2. ピタゴラス数を覚える
3. 一辺の長さしかわからない場合は角度に注目する
4. 一番長い辺が斜辺になることに注意する

ポイントをしっかり押さえて、三平方の定理の理解を深めましょう。

1.特別な直角三角形

三平方の定理を使う際「特別な直角三角形」の性質を覚えておくことは非常に役立ちます。

以下の三角形を、特別な直角三角形と呼びます。

  
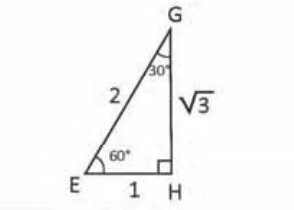
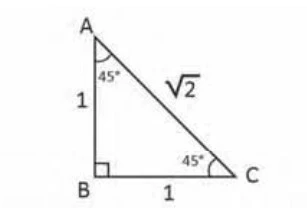
画像引用：国際協力機構「ピタゴラスの定理」P136

30°・60°・90°の直角三角形や45°・45°・90°の直角二等辺三角形には、特有の辺の比があります。特別な直角三角形の辺の比を覚えておくと、問題が効率よく解けて便利です。

たとえば、30°・60°・90°の直角三角形では、辺の比が1：2：√3となり、1辺の長さがわかれば残りの辺の長さも簡単に計算できます。

45°・45°・90°の直角三角形では、辺の比が1：1：√2です。この比を覚えておけば、計算の手間が省けるため、時間がかかりがちな問題もスムーズに解けるようになります。

逆に、三角形の比が1：2：√3なら30°・60°・90°の直角三角形、1：1：√2なら45°・45°・90°の直角三角形です。

特別な直角三角形の性質を頭に入れておけば、三平方の定理ですぐに解ける問題が増えるため、確実に覚えておきましょう。

2.ピタゴラス数を覚える「ピタゴラス数」を覚えておくことも、三平方の定理の問題に役立ちます。

ピタゴラス数とは、三平方の定理を満たす整数の組み合わせで、よく出題される比は効率よく覚えておくと便利です。

覚えておきたいピタゴラス数は、以下の4つです。語呂合わせもあわせて参考にしてください。

三辺の比	語呂合わせの例
3：4：5（直角三角形）	（み）（よ）（こ）ちゃん
5：12：13	（こ）（いつ）が（とうさん）
7：24：25	（な）（によ）（ニャンコ）
8：15：17	（は）（いご）で（じゅうなん）たいそう

とくに、3：4：5のピタゴラス数はもっとも有名で、3つの辺の比が3：4：5になっていれば、必ず直角三角形になります。

ピタゴラス数を覚えておけば、問題をみた瞬間に解答の道筋が立てやすくなります。紹介した語呂合わせを参考に、自分に合った覚え方を見つけてみましょう。

3.1辺の長さしかわからない場合は角度に注目する

直角三角形の1辺の長さしかわからない場合は、角度に注目しましょう。

三平方の定理では、2辺の長さがわかれば残りの1辺を求められます。しかし、1辺しかわからない場合、三角形の角度に注目して特別な直角三角形の比を利用する方法が有効です。

たとえば、1つの角度が60°である場合、残りの角度は30°となり、30°・60°・90°の直角三角形であると判断できます。この特別な三角形の辺の比は1：2：√3であるため、1辺の長さがわかれば、ほかの2辺の長さも簡単に計算できます。

角度に注目することで、1辺の長さしかわからない問題でも三平方の定理を使って解くことが可能です。

4.一番長い辺が斜辺になることに注意する

三平方の定理を使うときは、一番長い辺が斜辺になる点に注意しましょう。

直角三角形では、斜辺が一番長い辺であり、三平方の定理では常に斜辺をcとして公式に当てはめます。当てはめる箇所を間違えると、すべての計算がずれてしまい、正確な答えを導き出せません。

三平方の定理では「必ず一番長い辺が斜辺=c」であることを意識しましょう。基本的なポイントを押さえれば、三平方の定理を使いこなし正確に問題を解けるようになります。

三平方の定理を使った問題の解き方を解説

三平方の定理を使った問題の解き方を解説します。

実際に問題を解き、基本問題から複雑な問題への適用方法を理解しましょう。

問題例1
次の図で、Xの値を求めなさい。

 
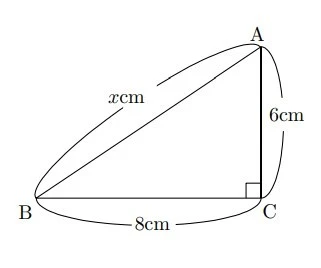
画像引用：足立区「中学3年 7章 三平方の定理」P45（1）

問題例2
次の図で、Xの値を求めなさい。

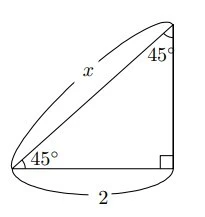
画像引用：足立区「中学3年 7章 三平方の定理」P47（1）

問題例3
3辺の長さが4、5、6である三角形は、直角三角形であるといえますか。

問題例4
次の図のXとyの値を求めなさい。

 
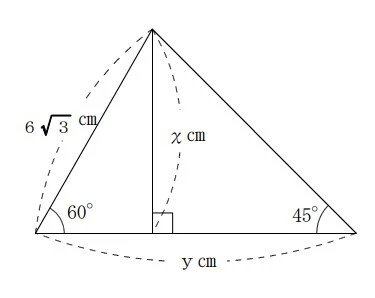
画像引用：千葉県「数学3 7章 三平方の定理 「三平方の定理の利用」＜基本問題＞」P9

・
・
・問題例1【解答】
ABは斜辺であるから、6² + 8² = X²
X² = 100
X > 0であるから、X = 10

答え　10cm

問題例2【解答】
特別な直角三角形の 3 辺の比を利用します。
1 : √2= 2 : Xより
X = 2√2

答え　X = 2√2

問題例3【解答】
三平方の定理の逆を利用します。直角三角形は斜辺が一番長いため、a = 4、b = 5、c = 6を公式に当てはめます。

a2 + b2 = 42 + 52 = 41
c2 = 62 = 36

a²＋b²＝c²という関係が成り立たないため、直角三角形といえません。

答え　直角三角形といえない

問題例4【解答】
直角三角形を左右で分けて考えましょう。
左側の直角三角形の角度に注目すると、特別な直角三角形であることがわかります。

X ： 6√3 = √3：2
2X = 18
X = 9

左側の直角三角形で2辺がわかったため、三平方の定理を利用しましょう。

a：6√3 = 1：2
a = 3√3 

次に、右側の直角三角形をみてみると、2つの角度より特別な直角三角形だといえます。

b = X = 9

y = b+a = 9+3

答え　x = 9　 y=9+3√3

まとめ

三平方の定理は、数学の中でも重要な公式であり、日常生活やさまざまな分野で応用されています。

三平方の定理を理解することで、複雑な問題を効率的に解く力が身につき、数学に対する自信も高まります。

ただ公式を使うだけではなく、まずは三平方の定理の証明で理解を深め、さまざまな問題に応用していきましょう。

もし、まだ不安や疑問が残っているなら、次のステップに進むチャンスです。ひとりで悩まず、適切な指導を受ければ、苦手を克服でき、数学への意欲も高まるでしょう。

森塾では、あなたの疑問に寄り添う丁寧な個別指導を行っています。理解ができるまでとことんサポートし、一緒に目標達成を目指します。

少しでも興味がある方は、ぜひ森塾の"無料"体験にお申込みください。

＞＞【お申し込み】森塾の"無料"体験はこちらから