空間図形とは？

空間図形とは、平面図形とは異なり、3次元空間に存在する図形のことを指します。空間図形は、一般的に立体図形とも呼ばれ、特徴は平面図形に「高さ」が加わることです。

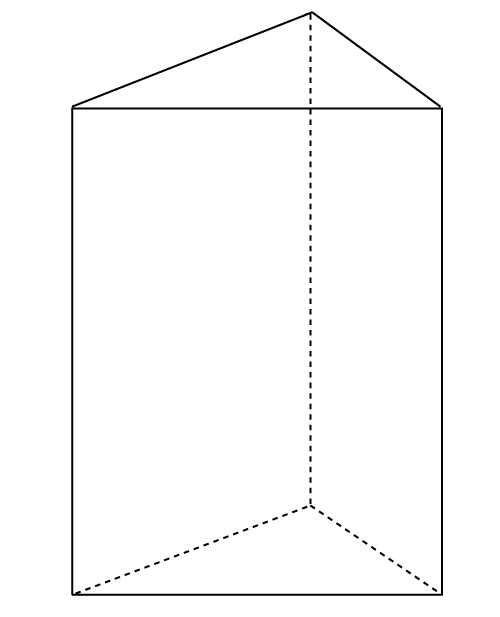
たとえば、三角形や四角形に高さが加わると、それぞれ三角柱や四角柱となり、円に高さを加えると円柱が生まれます。

空間図形は、平面図形に比べて構造や形状をイメージすることが難しく、苦手な学生は多い傾向にあります。

空間図形の理解を深めるためには、図形の各要素がどのように空間で配置されるかを具体的にイメージすることが重要です。

空間図形の解き方の基本！立体の名前や体積を求める公式を覚えよう

空間図形の問題を効率的に解くためには、立体の名前と基本的な公式を正確に覚えることが不可欠です。

空間図形の解き方に必要な知識を身につければ、複雑な問題でも自信をもって取り組めるようになります。

まず、空間図形の問題ででてくる図形の種類を「〜すい」と「～柱」の2つに分類します。

分類	例	特徴
～すい	円すい　　　　三角すい　　　　四角すい	てっぺんがとがっている
～柱	円柱　　　　三角柱　　　　四角柱	てっぺんが底面と同じ形

画像引用：教材で使えるイラスト素材

分類を押さえたうえで、空間図形の問題を解く際に重要な公式を紹介します。

 

対象	公式
円周	2πr（直径×3.14）
円の面積	πr²（半径×半径×3.14）
おうぎ形の弧の長さ	2πr×中心角/360°（円周×中心角/360°）
おうぎ形の面積	πr²×中心角/360°（円の面積×中心角/360°）
柱体の表面積	（底面積 × 2）＋（底面の周の長さ×高さ）
柱体の体積	底面積×高さ
すい体の表面積	底面積＋（底面の周の長さ × 斜高 ÷ 2）
すい体の体積	（底面積×高さ）×1/3
球の表面積	4πr²（4×半径×半径×3.14）
球の体積³	4/3 πr³（×半径×半径×半径×3.14）

公式を確実に覚えることで、空間図形の問題解決の基礎が固まります。しかし、単に暗記するだけでなく、それぞれの公式がなぜそうなるのかを理解することも大切です。

たとえば、柱体の体積が「底面積×高さ」となるのは、底面の形を高さ分積み重ねたものが柱体だからです。

空間図形の問題に取り組む際は、与えられた図形が「～すい」なのか「～柱」なのかを見極め、適切な公式を選択することから始めましょう。

問題文から必要な情報を丁寧に拾い出し、選んだ公式に当てはめていくことで、正確な解答を導き出せます。

空間図形の解き方で押さえておきたい4つのコツを紹介

空間図形の解き方で押さえておきたいコツは以下の4つです。

1. 立体を平面に変換する
2. ねじれの位置に気をつける
3. 切断面の法則を覚える
4. わかっている情報は図に書き込む

解き方のコツをしっかりマスターし、空間図形に対する苦手意識をなくしましょう。

1.立体を平面に変換する

空間図形の問題を解く際、もっとも効果的な方法が、立体を平面に変換して考えることです。

立体を頭の中で正確にイメージするのは難しいため、平面図形に分解することで理解がしやすくなります。

たとえば、円柱を考えるとき、底面とてっぺんに2つの円があり、側面は長方形として分解できます。円すいでは、底面にひとつの円、側面をおうぎ形とみなすことが可能です。

立体を構成する要素を平面図形に変換すれば、問題がシンプルに考えやすくなります。まずは、平面図形に分解して考えるクセをつけましょう。

平面図形が難しいと感じている方は、こちらの記事を参考にし、基本を復習してみてください。

「平面図形 解き方」の記事へ内部リンク（9月納品記事）

2.ねじれの位置に気をつける

空間図形の解き方では、直線同士の「ねじれの位置」にも注意しましょう。

ねじれの位置とは、2つの直線が平行ではないのに交わらない状態のことです。ねじれの位置の特性を理解しておくと、空間図形の直線の位置関係が把握しやすくなります。

たとえば、同じ平面上にない直線が、どれだけ延長しても交わらない場合は、ねじれの位置にあります。

あわせて平行と垂直についても理解しておきましょう。

• 平行：同じ平面上にある直線がどこまで伸ばしても交わらない状態
• 垂直：2つの直線が直角（90度）に交わる状態

問題例として、以下のような問題が挙げられます。

（1）下の図のような正四角柱があります。辺CDとねじれの位置にある辺をすべて答えなさい。

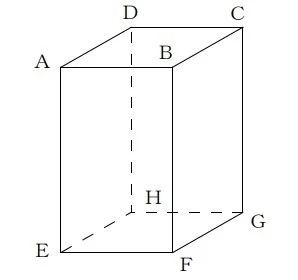
画像引用：佐賀県教育センター「中学校数学 第1学年 6 空間図形 （問題）」 P3 

【解答】辺BC、辺DC、辺FG、辺HG 

出典：佐賀県教育センター「中学校数学 第1学年 6 空間図形 （問題）」 P3

ねじれの位置、平行、垂直の違いをしっかり理解し、それぞれの関係を意識して問題に取り組んでみましょう。

3.切断面の問題を解くためのポイントを覚える

空間図形の問題で頻出するのが、立体を切断した際にあらわれる「切断面」の問題です。

切断面の問題を解くためには、以下のポイントを理解しておく必要があります。

• 同じ面にある点を結ぶ
• 向かい合う面の切り口は平行になる
• 斜めに切断した場合は、立体の辺も伸ばし大きな三角すいをつくる

切断面では、同じ面上にある点を結ぶことが基本です。また、対向する面の切り口は平行になり、斜めに切断した場合は立体の辺を延長することで、新たな三角すいをつくれます。 

立体の辺を延長する例は、以下の図を参考にしてください。

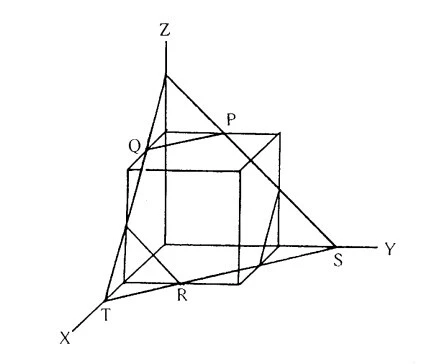
画像引用：国立情報学研究所 茨城大学教育学部紀要（教育科学）「立方体を平面で切ったときの切り口」の指導（中1）に取り入れる 操作・実験・コンピュータシミュレーションの効果の比較

上記の図で、点P、Q、Rが与えられていて、3点を通る切断面を作成します。

1. PQと平行になる直線を引き、Y軸との交点をSとする。
2. SRの延長線とX軸の交点をTとし、TとQを通る直線を引く。
3. SとPを通る直線を引く。
4. 交点同士を結ぶと、切断面の作図ができる。

出典：国立情報学研究所 茨城大学教育学部紀要（教育科学）「立方体を平面で切ったときの切り口」の指導（中1）に取り入れる 操作・実験・コンピュータシミュレーションの効果の比較

空間図形の切断面に関する問題は、ポイントを押さえて正しく処理すれば、スムーズに解けるようになります。

4.わかっている情報は図に書き込む

空間図形の問題を解く際、与えられた情報を図にしっかりと書き込むことが大切です。

平面図形と同じように、問題で与えられた辺の長さや角度などの情報をすぐに図に反映すれば、解答への手がかりが得られます。

また、正確な立体図形の作図は重要です。見えない部分や奥行きは点線で表現し、理解しやすい図を作成すれば、問題の複雑さが軽減されます。

空間図形の問題を解く際には、わかっている情報をすべて書き込み、視覚的に整理する習慣をつけるようにしましょう。

空間図形の解き方を練習しよう！実際の問題と解答

最後に、実際に出題される問題を解いてみましょう。

問題1

（1）次の図1は円柱の見取り図で、図2はその展開図です。円Oの半径は3cmです。

展開図の長方形の辺ADの長さを求めなさい。円周率はとする。

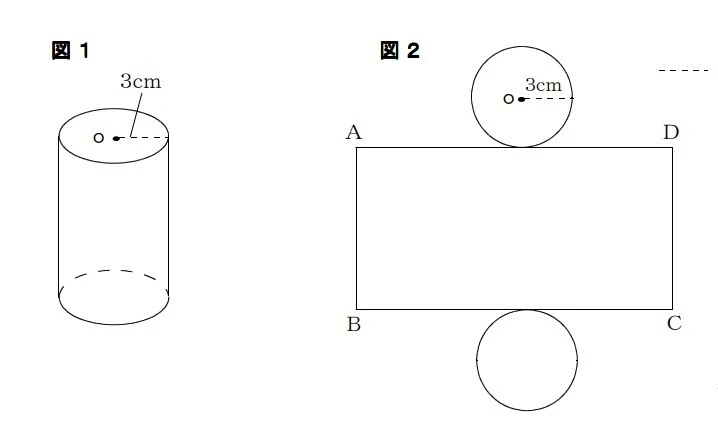
画像引用：佐賀県教育センター「中学校数学 第1学年 6 空間図形 （問題）」

（2）次の円すいの展開図をかくと、側面はどのような図形になりますか。

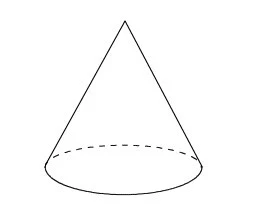
画像引用：佐賀県教育センター「中学校数学 第1学年 6 空間図形 （問題）」

問題2

下の直方体について、次の問いに答えなさい。

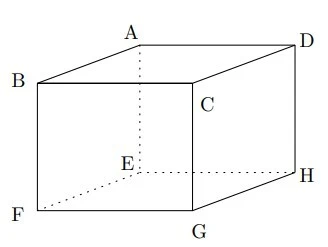
画像引用：足立区「中学1年数学 7章 空間図形」

（1）面ABCDに垂直な辺をすべていいなさい。

（2）辺ABと平行な面をすべていいなさい。

（3）辺ABとねじれの位置にある辺をすべていいなさい。

問題3

長方形を1回転させて立体をつくりました。

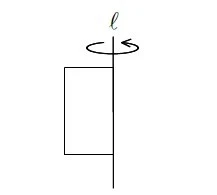
画像引用：佐賀県教育センター「中学校数学 第1学年 6 空間図形 （問題）」

（1）この立体の見取り図をかきなさい。

（2）この立体を、軸を含む平面で切ると、切り口はどのような図形になりますか。また、軸に垂直な平面で切ると、切り口はどのような図形になりますか。それぞれ答えなさい。

・

・

・

【解答】 

問題1

（1）展開図の長方形の辺ADの長さを求めなさい。

解答　6cm

【ポイント】

 展開図の長方形の横の長さと、円周の長さは等しくなる

（円周の長さ）=（直径）×π

3×2×π ＝6π

（2）次の円すいの展開図をかくと、側面はどのような図形になりますか。

解答　おうぎ形

問題2

（1）面ABCDに垂直な辺をすべていいなさい。

解答　辺AE、BF、 辺CG、 辺DH

（2）辺ABと平行な面をすべていいなさい。

解答　面EFGH、面CGHD

（3）辺ABとねじれの位置にある辺をすべていいなさい。

解答　辺CG、辺DH、 辺EH、 FG 

問題3（1）この立体の見取り図をかきなさい。

解答

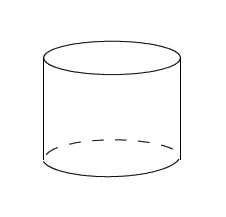
画像引用：佐賀県教育センター「中学校数学 第1学年 6 空間図形 （解答例）」 P4

【ポイント】

長方形を回転させると、円柱になります。

（2）この立体を、軸を含む平面で切ると、切り口はどのような図形になりますか。また、軸に垂直な平面で切ると、切り口はどのような図形になりますか。それぞれ答えなさい。

解答

軸を含む平面で切るとき：長方形

軸に垂直な平面で切るとき：円

まとめ

空間図形の問題は、最初は難しく感じるかもしれません。

しかし、立体を平面に変換する考え方や各立体の体積を求める公式、解き方のコツをしっかりと理解すれば、空間図形の問題もスムーズに解けるようになります。

複雑な問題にも対応できるように、くり返し問題を解いていきましょう。

まだ不安な箇所がある、さらにじっくり解説してほしいと感じた方は、森塾の無料体験を受けてみてください。

森塾では、あなたと相性のよい講師が、丁寧な個別指導でサポートします。一人ひとりの理解度にあわせた学習ができるため、苦手を克服しながら確実に力を伸ばせます。

ぜひお気軽に"無料"体験にお申込みください。

＞＞【お申し込み】森塾の"無料"体験はこちらから