「平面図形の解き方がわからない」「図形の問題を見ただけで頭が真っ白になる」など、中学1年の数学で習う平面図形に苦手意識をもってしまう方は多いでしょう。
本記事では、三角形・四角形・円といった基本的な平面図形の性質から、面積や周長の求め方と解き方のコツまで丁寧に解説していきます。
練習問題も用意しているため、内容を理解したうえでぜひ挑戦してみてください。
- 平面図形の解き方の基本が理解できる
- 平面図形の種類や公式がわかる
- 平面図形の解き方で重要な4つのコツがわかる
平面図形の解き方の基本

平面図形は、高さと幅からなる平面上に描かれた図形です。空間図形とは、奥行きを考えない点が異なります。
はじめて見る平面図形の問題は、難しそうに感じるかもしれません。しかし、用語を覚えたり、図形上で公式が使えるポイントを探したりすれば、簡単に解けるようになるはずです。
そこで、以下3つの基本的な内容を解説していきます。
- 平面図形の種類と性質
- 覚えておくべき用語と記号
- 平面図形の解き方で使う公式
中学1年から学ぶ平面図形の知識は、中学2年生で学ぶ「図形の証明」や、中学3年生の「図形の相似」でも必須です。中学1年生で基礎を固めて、次の学年に備えましょう。
空間図形の解き方|基本の考え方と押さえておきたい4つのコツを紹介
平面図形の種類と性質
平面図形で登場する図形は、次の5種類に分けられます。特徴や性質をまとめたので、問題を解くときの参考にしてみてください。
|
分類 |
|
例 |
特徴 |
|
三角形 |
正三角形 |
|
3辺の長さが等しい |
|
直角三角形 |
|
1つの内角が直角(90°) |
|
|
二等辺三角形 |
|
2辺の長さが等しい |
|
|
四角形 |
長方形 |
|
4つの角がすべて直角 |
|
正方形 |
|
4つの角がすべて直角・4つの辺の長さが等しい |
|
|
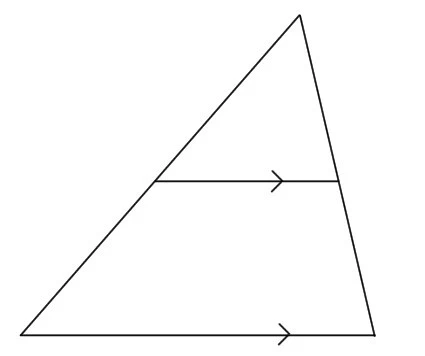
平行四辺形 |
|
向かい合う辺2組がそれぞれ平行 |
|
|
台形 |
|
向かい合う辺1組が平行 |
|
ひし形 |
|
4つの辺の長さが等しい |
|
円 |
|
定点から等距離にある点の集合 |
|
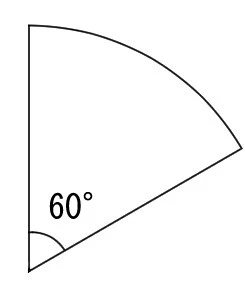
おうぎ形 |
|
円の2本の半径とその間にある円弧で囲まれた図形 |
覚えておくべき用語と記号
平面図形の問題を解くには、用語と記号を覚えることが大切です。難しく感じる問題でも、問題文に書かれた用語を読み解けば、解法のヒントがつかめるかもしれません。
そこで、図形問題によく出る用語を、次にまとめました。
|
分類 |
例 |
特徴 |
|
|
直線 |
直線 |
|
両側に限りなく伸びる直線 |
|
線分 |
 |
長さが決まっている直線 |
|
|
半直線 |
 |
片側に限りなく伸びる直線 |
|
|
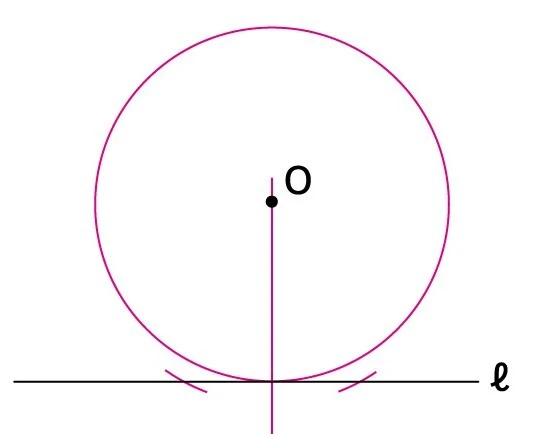
接線 |
|
1点で円に接する直線 |
|
|
点 |
中点 |
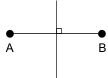 |
線分を2等分する点 |
|
交点 |
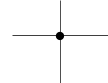 |
直線同士が交わる点 |
|
|
接点 |
 |
円と接線が接する点 |
|
|
角 |
角 |
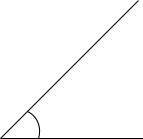 |
2直線がつくる角 |
|
中心角 |
|
円の2つの半径が挟む角 |
|
|
平行 |
|
交わらない2直線 |
|
|
垂直 |
垂直 |
 |
2直線の交わる角度が90°である |
|
垂線 |
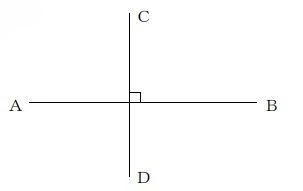 |
直線と垂直に交わる直線 |
|
|
垂直二等分線 |
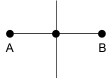 |
線分の中点と垂直に交わる直線 |
|
|
弦と弧 |
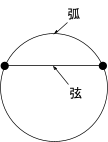 |
弧:円周上の一部分 弦:円周上の2点を結ぶ線分 |
|
また、平面図形で使用される記号についても、以下にまとめました。
|
意味 |
記号 |
|
A、B、Cを頂点とする三角形 |
△ABC |
|
△ABCの頂点B部分の角度 |
∠ABC |
|
2直線ABとCDが交わってできる角が90°(直角) |
AB⊥CD |
|
2直線ABとCDが平行(交わらない) |
AB//CD |
|
2点A、Bを両端とする弧 |
A͡͡͡͡͡͡͡͡͡͡B |
平面図形の解き方で使う公式
平面図形の問題を解くうえで必要な公式は、次の通りです。
|
対象 |
公式 |
|
|
三角形の面積 |
正三角形 |
底辺×高さ÷2 |
|
直角三角形 |
||
|
二等辺三角形 |
||
|
四角形の面積 |
長方形 |
横×縦 |
|
正方形 |
1辺×1辺 |
|
|
平行四辺形 |
底辺×高さ |
|
|
台形 |
(上底+下底)×高さ÷2 |
|
|
ひし形 |
対角線×対角線÷2 |
|
|
円 |
直径の長さ |
2r |
|
円周の長さ |
2π(直径×円周率) |
|
|
円の面積 |
πr²(半径×半径×円周率) |
|
|
おうぎ形 |
弧の長さ |
2πr×中心角/360°(円周×) |
|
面積 |
πr² ×中心角/360°(円の面積×) |
|
|
中心角の大きさ |
360°×((弧の長さ))/2πr(中心角の比=弧の長さの比) |
|
平面図形の解き方で重要な4つのコツ

平面図形の問題を解くには、次のコツを押さえましょう。
- わかっている情報を書き込む
- 補助線を引いて工夫する
- 公式が使える部分を探す
- 作図は正確に行う
1.わかっている情報を書き込む
問題を解き始める前に、問題文の情報を図に書き込みましょう。書き込む工程を省くと、問題を解くヒントが得られないため、忘れないように注意してください。
辺同士の関係(平行・垂直、長さが同じなど)や角度など、図に書かれていない情報を記入しましょう。情報を書き込むと、新しい情報が見えてくるので、さらに書き込みを続けてください。
書き込みが終わったら、図形の特徴や相似・合同などの公式・定理を使って、追加の情報を手に入れましょう。最初の書き込みを丁寧に行うことで、答えにつながるヒントを得られるかもしれません。
2.補助線を引いて工夫する
複雑に見える図形でも、1本補助線を引くだけで解けることもあります。二等辺三角形や平行四辺形ができるように、補助線を引いてみましょう。公式や性質がわかる図形を作り出すことで、解法を見つけられる可能性もあります。
補助線の引き方は、次の4通りです。
|
補助線の引き方 |
|
|
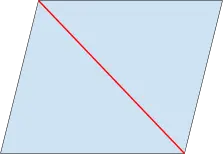
1.頂点と頂点を結ぶ |
 |
|
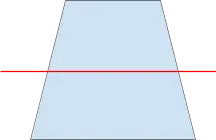
2.辺に対して平行・垂直な線を引く |
 |
|
3.線を延長する |
 |
|
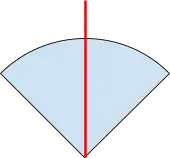
4.円やおうぎ形の中心から弧に向けて線を引く |
 |
3.公式が使える部分を探す
問題文の情報や、図形の性質・関係性の情報をもとに、どのような公式が使えそうか考えましょう。
使える公式を探す工程は、平面図形の問題でもっとも大切なポイントです。面積を求めたい図形に使えそうな公式を思い浮かべて、計算に必要な辺の長さ・角度がすべて揃っているか、チェックしてみてください。
平面図形の問題を解くには、図形の名前と、対応する公式を覚える必要があります。基礎を怠らず、公式をしっかり覚えてください。
4.作図は正確に行う
平面図形の問題では、作図を求められることもあります。次のような作図ができるよう、練習しておきましょう。
- 垂直二等分線の作図
- 角の二等分線の作図
- 垂線の作図
作図問題では、書いた線の跡をもとに、正解しているか判断します。最終的な形が同じでも、正しい作図の跡がなかった場合は、正解になりません。作図に用いた線は、消さずに残しましょう。
また、作図に使う道具を忘れないように注意してください。コンパスや定規は、常に筆箱に入れておくのがおすすめです。
平面図形の問題と解答 解き方を実践してみよう

平面図形の問題を解くには、問題に慣れることが重要です。解き方のコツを押さえて、実際の問題を解いてみましょう。
【問題1】右の図は、2本の直線AB、CDが垂直に交わっています。
これを記号を使って表しなさい。

画像引用:佐賀県教育センター「中学校数学第1学年5 平面図形[問題]」| P2
【問題2】おうぎ形で、2つの半径のつくる角を何といいますか。
【問題3】線分 AB 上の点 P を通り、AB に垂直な直線を作図しなさい。
【問題4】 下の図のように半径が6cm、弧の長さが4πcmのおうぎ形があります。このおうぎ形の面積を求めなさい。
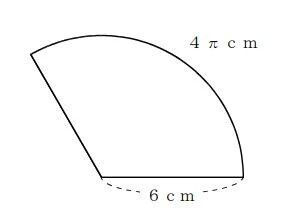
画像引用:佐賀県教育センター「中学校数学第1学年5 平面図形[問題]」| P5
【解答】
問題1:AB⊥CD
問題2:中心角
問題3
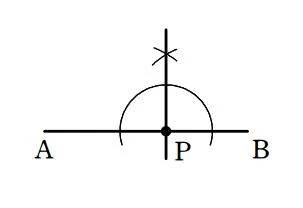
問題4
まず中心角を求める。
中心角の比=弧の長さの比なので、「360°:(中心角)=2×6×π:4π」
よって、中心角の大きさは120°
したがって、おうぎ形の面積は
π×6²×120°/360°=12π(cm²)
まとめ

平面図形の問題は、図や問題文を見ると一見複雑そうに感じますが、用語や公式を正しく覚え、図形の性質を理解すれば簡単に解けるようになります。
平面図形の解き方は、これから先に習う単元でも必要になる重要な要素です。わかっている情報を書き込み、覚えた公式を適切に使用してどんどん練習問題を解いていきましょう。
- 平面図形の問題を解くためには、図形の名前や用語、公式を正しく覚えることが重要
- わかっている情報は書き込んだり、補助線を引いたりといった工夫するのがコツ
- 作図は正確に書けるように練習し、どんどん図形問題に慣れることが大切
さらにじっくり解説してほしい、ほかの分野も理解できるようになりたいと感じた方は、森塾の無料体験を受けてみてください。
森塾では、森塾では生徒一人ひとりの理解度に合わせた丁寧な指導を行っています。理解ができるまでとことんサポートを受けられ、確実に力を伸ばすことができます。
少しでも興味がある方は、ぜひ"無料"体験にお申込みください。