因数分解は中学3年生で学ぶ重要な単元です。共通因数や定数項など新しい概念と複数のテクニックを必要とするため、苦手意識をもちやすいです。
この単元は、同じく中学3年で学ぶ二次方程式や高校で習う三次方程式にも直結するため、しっかりと身につけておきましょう。
本記事では因数分解の基礎知識や、解くのに必要な手順とコツを解説しますので、苦手を克服するきっかけとしてみてください。
- 因数分解の基礎知識
- 因数分解の公式
- 因数分解を解くための手順やコツ
そもそも因数分解とは何か?

因数分解とは、足し算や引き算が混ざっている数式をカッコでまとめて、かけ算の形にすることです。
たとえば、x² + 3x + 2を因数分解すると以下になります。
x² + 3x + 2 = (x + 1)(x + 2)
上の式では、足し算や引き算の式がかけ算の式の形になっていますよね。
これに対して、(x + 1)(x + 2) = x² + 3x + 2のように、カッコでくくられたかけ算の式を足し算や引き算の形に変形することを展開と言います。
因数分解を使う理由

因数分解を利用するのは、中3で習う二次方程式や高校で習う三次方程式の解答を導きやすくするためです。
たとえば、次の二次方程式を解いてみましょう。
x² + 3x + 2 = 0
この状態のままでは、xの値を求めるのは難しいですよね。
しかし、この数式を以下のように因数分解すれば解答しやすくなります。
(x +1)(x + 2) = 0
この式の場合、2つあるカッコのどちらかがゼロになれば正解です。
カッコの中がゼロになるケースは、以下の2通りです。
x + 1 = 0
x + 2 = 0
つまり、この式のxの値は
x = −1、x = −2
となります。
つまり、因数分解をすることで、二次方程式を一次方程式に分解できるため、問題が解きやすくなるのです。
なお「子どもが二次方程式を解けない」と、お悩みの方は以下の記事でくわしく解説していますので参考にしてみてください。
二次方程式の解き方をわかりやすく解説|中学生によくあるミスも紹介
中学生で習う因数分解の公式一覧

因数分解を解くには、以下の公式を覚える必要があります。
- x² + (a + b) x + ab = (x + a)(x + b)
- x² − y² = (x + y)(x − y)
- x² + 2xy + y² = (x + y)²
- x² − 2xy + y² = (x − y)²
3と4は符号以外は同じなので、どちらかを覚えておけばよいです。つまり、覚えなければいけない公式は3つだけです。
因数分解の問題では、使用すべき公式を指示されることはありません。問題を見てどの公式を使うべきか判断する必要があります。演習を重ねれば、どの公式を使うべきかパズルを解くように判断できるようになります。コツコツ取り組めば、因数分解のコツがつかめてきますよ。
次の章では、どの公式を使えばいいのか検討をつけるコツや公式が使えなくても簡単に解く方法について解説します。
因数分解を解くときの方法とコツ

因数分解を解くときの方法は、以下のとおりです。
- ・共通因数でくくれるか調べる
- ・公式に当てはめる
- ・数式を置き換える
- ・たすき掛けを利用する
順番に解説します。
共通因数でくくれるか調べる
まずは、数式の中に共通因数がないか調べましょう。共通因数とは、式の中でいくつかの項に同じように登場する数字や文字のことです。
6x² + 3x
という式があった場合、共通する文字は「x」共通する数字は「3」です。
その次に、共通因数をカッコの外にくくり出し、答えは以下になります。
3x(2x + 1)
公式に当てはめる
たとえば、x² + 2x + 1のように共通因数がない場合は、因数分解の公式が使えないか確認します。
どの公式が使えそうか判断するには、項の数に注目するとよいです。項とは足し算や引き算の記号で分けられる、式の中の一つひとつのパーツを指します。x²-36の場合、項は「x²」と「-36」の2つです。
項の数が2つの場合は、x² − y² = (x + y)(x − y)の公式が使えないか見てみます。
x²-36は、x²はxを36は6を2乗しているため、公式に当てはめると答えは以下のようになります。
x²-36=(x + 6)(x − 6)
続いて、x² − 8x + 16 のように項の数が3つの場合は、以下の公式のいずれかを使います。
- x² + (a + b) x + ab = (x + a)(x + b)
- x² + 2xy + y² = (x + y)²
- x² − 2xy + y² = (x − y)²
検討の付け方としては、真ん中の項が2で割れるかどうかです。
x²− 8x + 16 の場合、−8を2でわると−4になります。次に、この数を2乗すると3つ目の項と同じになれば、2か3の公式に当てはめることができます。今回は「−4」を2乗すると16になるので、3の公式が使え、以下のように因数分解が可能です。
x²− 8x + 16=(x − 4)²
上記のパターンでない場合、つまり真ん中の項が2で割れないときや、割れた数を2乗しても3つ目の項二ならない場合は、1の公式を使いましょう。
たとえば、以下のような問題です。
x² + 3x + 2
この場合、真ん中の項である3は2で割れないため、1の公式を使います。
x² + (a + b) x + ab = (x + a)(x + b)
この公式の考え方は、足して3、かけて2になる数字の組み合わせがないか考えればいいわけです。よって答えは以下のようになります。
x² + 3x + 2= (x + 1)(x + 2)
数式を置き換える
因数分解の公式が使えるものの、そのまま当てはめると計算しにくい場合、まずは文字に置き換えると解きやすいです、
たとえば以下のような問題です。
(2x +1)² + 3(2x +1) + 2
カッコ内の数字が同じであれば、カッコを同じ文字として置き換えます。たとえば「A」として置き換えたら
A² + 3A +2 = (A + 1)(A + 2)
と簡単に因数分解できます。そして、Aを置き換える前の数値に戻せば解答できます。
(2x + 1 + 1)(2x + 1 + 2) = (2x + 2)(2x + 3)
たすき掛けを利用する
共通因数でくくれない場合や、因数分解の公式が使えそうにない場合は、たすき掛けを利用します。
たとえば、以下のような問題です。
2x² + 7x + 3
考え方は、以下のとおりです。
- 因数分解はかけ算の形にするため、2x² + 7x + 3=( )( )の形がゴール
- まずは2x²に注目。2x²を作るためには(2x
- □)(x□)になる
- □に入る数字をたすき掛けで決める
□に入る数字をたすき掛けで決める方法は、以下のとおりです。
- 2x² + 7x + 3=(2x □)(x □)
- 因数分解は展開の逆なので、展開したときに2x² + 7x + 3になればよい
- つまり、かけて3になり、足して 7xになる組み合わせを見つける
- かけて3になる組み合わせは「3」「1」
- (2x □)(x □)のどちらに「3」どちらに「1」が入るかたすき掛けで決める
たすき掛けの方法は、以下の図のとおりです。
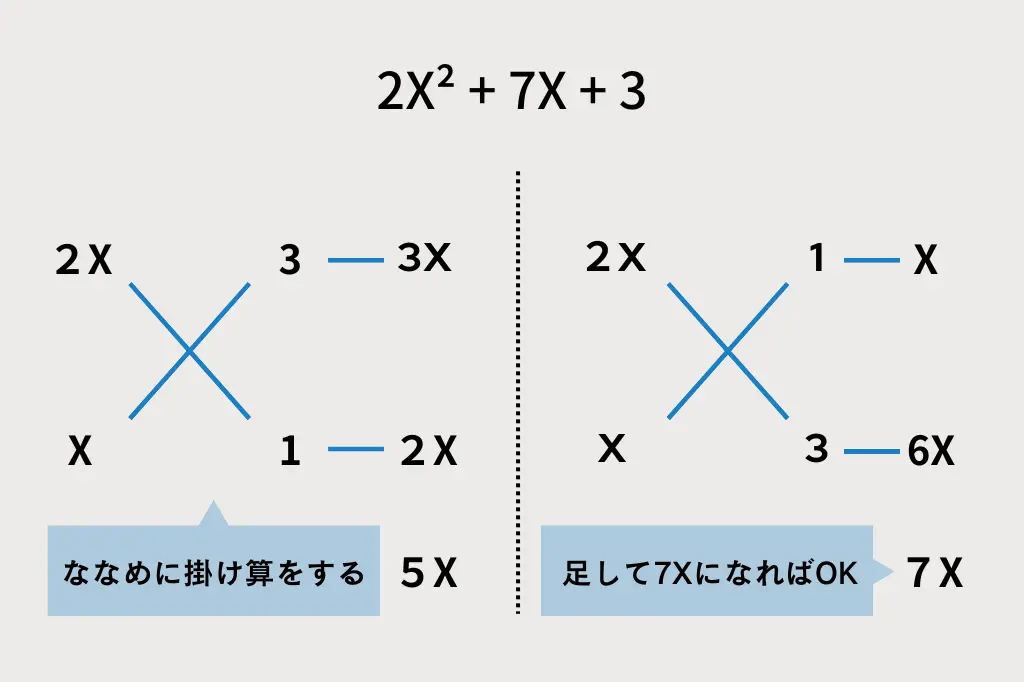
ななめに掛け算をして出た答えを足して、7xになるのは(2x + 1)(x + 3)の組み合わせになるため、答えは以下になります。
2x² + 7x + 3=(2x + 1)(x + 3)
まとめ:因数分解を解くには公式を覚えるまで繰り返しの演算が大切

因数分解を解くには、まずしっかりと公式を覚える必要があります。また、解答への手順まで理解しておけば、因数分解に対する苦手を解消するきっかけとなります。
この記事のまとめ- 因数分解とは、足し算や引き算が混ざっている数式をカッコでまとめて、かけ算の形にすること
- 因数分解の解き方は、共通因数でくくる方法、公式を使う方法、たすき掛けを利用する方法などがある
- 演習を重ねれば、どのパターンの問題かわかるようになってくる
因数分解はパズル的な要素が強く、慣れるのにコツがいります。コツを教えるのが難しいと感じるなら、早めに塾に通わせるとよいでしょう。
では、授業の理解度を確認する「クリアテスト(理解度テスト)」を毎回の授業開始時に実施しております。お子さんの理解度に合わせた指導で、因数分解のコツもわかりやすく教えます。
なかなか勉強が習慣化しない子どもでも、学習が続くような環境はどのようなものなのか、まずは"無料"体験で森塾の教育メソッドを体験してみませんか?