中学1年生で学ぶ「比例と反比例」について、式の求め方やグラフの書き方がわからず悩んでいる方もいるのではないでしょうか。
本記事では、比例と反比例の式の求め方やグラフの書き方、実際の問題例について紹介します。ぜひ本記事を参考にして、比例と反比例の理解を深めてみてください。
関数とは

比例と反比例を解説する前に、まずは関数について解説をします。関数とは「ある量の値が決まると、それに応じて別の量の値も決まる関係」を表現するものです。
関数という大きな概念のなかに「比例」と「反比例」があります。たとえば「Aが増えれば増えるほど、同じ量だけBが増える」という関係のことを「比例」といいます。一方で「Aが増えれば増えるほど、同じ量だけBが減る」という関係のことを「反比例」と呼びます。
比例・反比例とは

比例と反比例について、それぞれ式やグラフとあわせて解説します。
比例の式・グラフ
比例とは、2つの量の間に比例定数がある関係のことです。比例定数とは、2つの数の積が常に一定になる数のことです。
▼比例の式
y = ax
※aは比例定数
たとえば「ある国で1円の価値が2倍になると、その国の物価も2倍になる」という関係は、比例の関係といえます。この場合の比例定数は「2」であり、1円の価値が2倍になると、物価も2倍になるということです。この場合の比例式は「y = 2x」になります。
比例のグラフは、次のように直線になります。
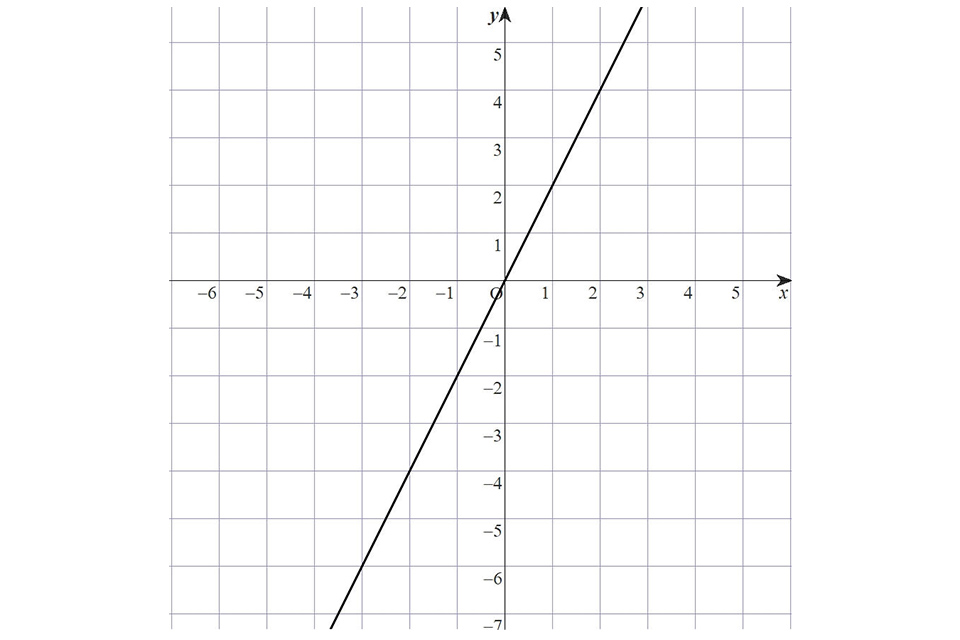
xの値が2倍3倍と大きくなればなるほど、yの値も2倍3倍と大きくなるのが特徴です。
反比例の式・グラフ
反比例とは、2つの量の積が常に一定になる関係のことです。比例とは異なり、2つの量は逆数の関係にあります。
▼反比例の式
y = a/x
※aは比例定数
たとえば雨が降ると、道路のぬかるみは深くなります。このときに「雨が増えれば降るほど、道路のぬかるみは深くなる(=道路の高さが低くなる)」というのは反比例の式で表すことができます。仮に雨が2倍、3倍になり、道路の高さが1/2倍、1/3倍になる場合は「y = 1/x」になります。
反比例の比例定数は「a = xy」で求めることも可能です。上記例の場合「2 * 1/2」で比例定数は「1」であることがわかります。
反比例のグラフは、次のように双曲線になります。
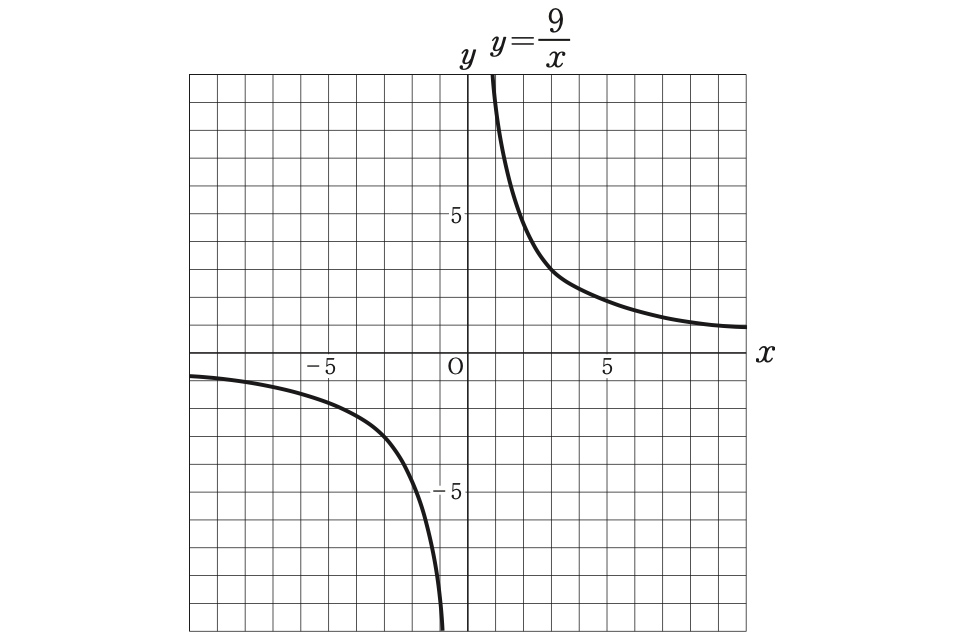
xの値が2倍、3倍と大きくなればなるほど、yの値は1/2倍、1/3倍と小さくなるのが特徴です。
比例・反比例の問題例

比例反比例に関する問題例をいくつか紹介します。あわせて解答も記載しますので、まずはゆっくり考えてから答え合わせをしてみてください。
問題①
問題:次のなかでyがxに比例しているものはどれか答えなさい。
A: y = - 4x
B: y = 2/x
C: y = 2/5x
D: y = 2x - 1
↓
↓
↓
↓
↓
↓
↓
解答:A、C
補足:比例は「y=ax(aは定数)」で表現するため、該当するものはAとCになります。
問題②
問題:下記それぞれの場合で、yをxの式で表しなさい。
A:yはxに比例し、x = 9のときy = 3である
B:yはxに反比例し、x = 5のときy = 1である
↓
↓
↓
↓
↓
↓
↓
解答:Aはy = 3x、Bはy = 5/x
補足:
Aについて、「y = ax(aは比例定数)」の式を求めれば良いため、aの値を算出します。
9 = 3a
↓a = 3
「a = 3」になるため「y = 3x」になることがわかります。
Bについて、「y = a/x」つまり「a = xy」の式を求めれば良いため、aの値を算出します。
a = 5 × 1
「a = 5」になるため「y = 5/x」になることがわかります。
問題③
問題:
何冊かのノートの束があり、その重さは4500gでした。このノートの重さは10冊で1500gです。このとき、次の問に答えなさい。
A:ノートx冊の重さをy gとしたとき、yをxの式で表しなさい。
B:束になっているノートの冊数を求めなさい。
↓
↓
↓
↓
↓
↓
↓
解答:Aはy = 150x、Bは30冊
補足:ノートの冊数と重さは比例関係にあり、定数は1冊あたりの重さになるため「y = 150x」ということがわかります。また、重さ(y)が4500gの場合、冊数(x)は30冊ということもわかります。
問題④
A:底辺6cm、高さxcmの平行四辺形の面積(y㎡)
B:底辺xcm、高さycmの三角形の面積(20㎡)
C:時速60kmで走る自転車が、x時間で走る道のり(y km)
D:30kmの道のりを時速






